應用分析模式
土石流模式SDF model
更新日期2021年10月21日
土石流模式SDF model參考 (Hunt 1994)提出的以完全發展層流(fully developed laminar flow)為流體模型進行土石流運動之模擬,假設坡面土石含水量達到飽和時,水分與泥砂較為均勻混和,而形成土石流流體後,沿著山區溪溝內之土石流移動,並且將複雜的土石流運動過程加以簡化,以增加演算的效率 (Chiang 2010)。假設野溪底床面和空氣為自由面零剪應力邊界時,土石流的速度剖面可寫成 (Chen et al. 2018; Hunt 1994):

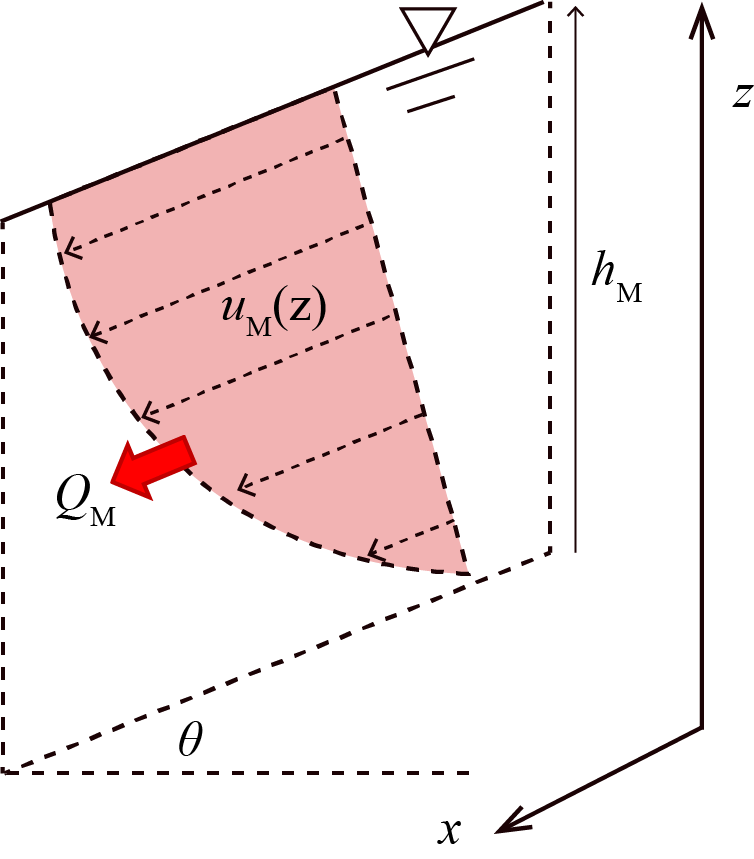
資料來源:轉繪自姜壽浩 (2010)
圖1 土石流流速剖面與其參數示意圖
其中,為土石流流速[m/s];z為土石流在垂直方向的空間位置[m];
為土石流流深 [m];
將式1的土石流速度流速剖面從底床到土石流表面進行積分,得到完全發展土石流的流量(QM)為:
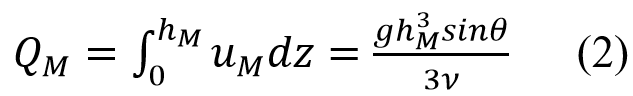
基於上述Hunt模式之基礎,以Matlab程式語言為基礎,撰寫成一套土石流模式。因其簡化複雜的土石流運動機制,且執行效率佳,稱為簡易土石流模式(Simplified Debris-Flow model,簡稱SDF-model)。
SDF-model所需要的初始條件分別為地形、土砂料源、運動黏滯係數、平衡濃度與演算時距,各個初始條件的說明如下:
♦地形:須輸入正規網格的數值地形模型(Digitial Terrain Model, DTM),模式演算過程皆將地形視為不變之剛體,不考慮土石流侵蝕河而產生的捲增效應,因此,在輸入數值地形模型時,需要根據使用者模擬需求,或土石流對地面物的衝擊程度,修正數值高程模型。
♦土砂料源:土砂料源的量體和空間位置是影響土石流運動最重要之因素,一般來說,土砂料源量體越大,土石流最終堆積範圍和深度通常越大;土砂料源越集中,土石流流動的範圍也就越遠。土石流的土砂料源可來自於崩塌、土壤沖蝕、或人工棄土等,其中崩塌為臺灣山區土石流最主要的土砂來源 (Chen et al. 2018)。崩塌的土砂量可藉由野外調查、數值地形模型相減、或崩塌體積和地形之間的經驗式進行推估,其中,較為被國、內外學者採用的方法為崩塌體積─面積關係式(volume−area relation):
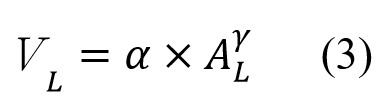
其中,VL為崩塌體積 [m3];AL為崩塌面積 [m2];α和γ為參數,須透過現地的崩塌樣本資料率定。藉由各地區發展的崩塌體積─面積關係式和觀測崩塌面積,便可推估崩塌體積。因SDF-model中需要輸入土砂料源的深度(單位公尺),則須將崩塌體積除以面積,得到每個崩塌的平均深度作為模式的初始參數。崩塌深度(DL)的計算式如下:

一般來說,當崩塌屬於岩盤材料時,γ介於1.3-1.6之間;當崩塌屬於土壤材料時,γ介於1.1-1.3之間。
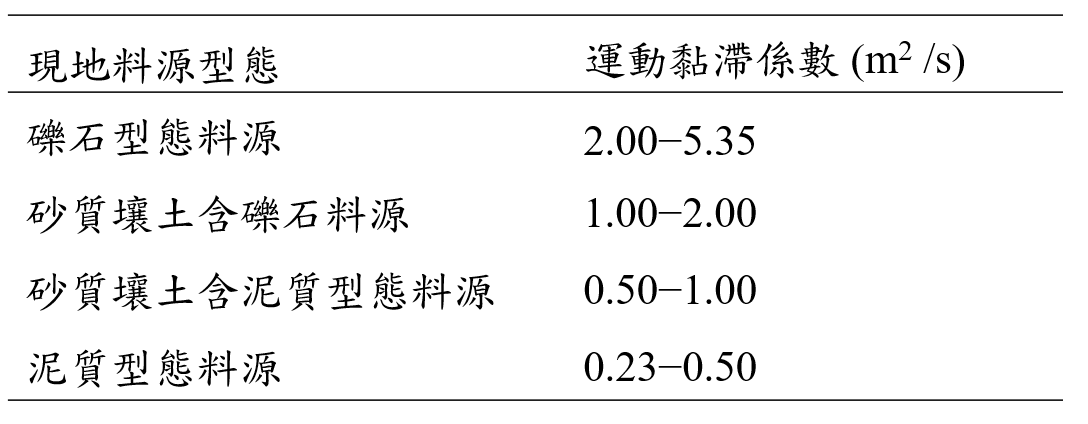
♦運動黏滯係數:是指流體在受到剪應力後流動的難易程度,泥流型土石流(mud flow)的運動機制主要為砂石則懸浮於泥水之中,流動性較佳;礫石型(granular flow)的運動機制以碰撞和滾動為主,泥水只扮演潤滑角色,流動性較差。故在模擬土石流的流動性時,可根據土石流現地料源的型態予以給定,表1為SDF-model建議之現地料源的型態對應運動黏滯係數。
表1 現地料源的型態對應運動黏滯係數建議值
♦體積濃度:平衡濃度(equilibrium concentration, Cd)是指土石流材料在流動中混合達到完全發展狀態時,即堆積層不產生侵蝕與堆積,則土石之濃度會趨於平衡狀態,此時泥砂在土石流體中所佔據的比例稱為土石流平衡濃度。Takahashi (1981)根據實驗結果,發現當坡度大於17.6度的河谷,理論體積濃度最大值為0.603。

其中,Cd為土石流中泥砂的體積平衡濃度;ρ為水的密度1.00 g/cm3;
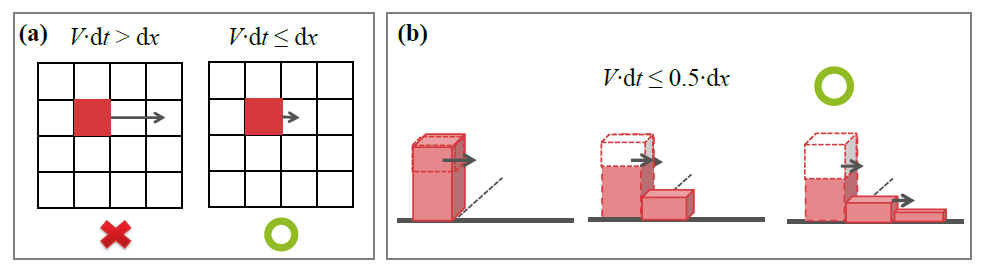
♦演算時距:指模式在演算一個步驟對應真實時間(dt),演算時距的概念可類比於Courant–Friedrichs–Lewy(CFL)的穩定條件,為避免土石流在一個步驟的移距離超過其鄰近八個網格,土石流移動距離(流速乘以演算時距)必須要小於網格大小(如圖2a),方能達到穩定。根據模擬的經驗,當演算時距小於0.5個網格大小,其模式較為穩定(如圖2b)。假設土石流最大流速(V)為20 m/s,若使用20 m × 20 m的數值地形模型,則建議的演算時距需 ≤ 0.5秒。
資料來源:Chen et al. (2018)
圖2 土石流模擬穩定條件和演算時距
土石流模式模擬結果經過BigGIS轉換模組處理後,可直接於BigGIS上呈現(圖4),可用於和其他圖資相互套疊比對分析(圖5)。
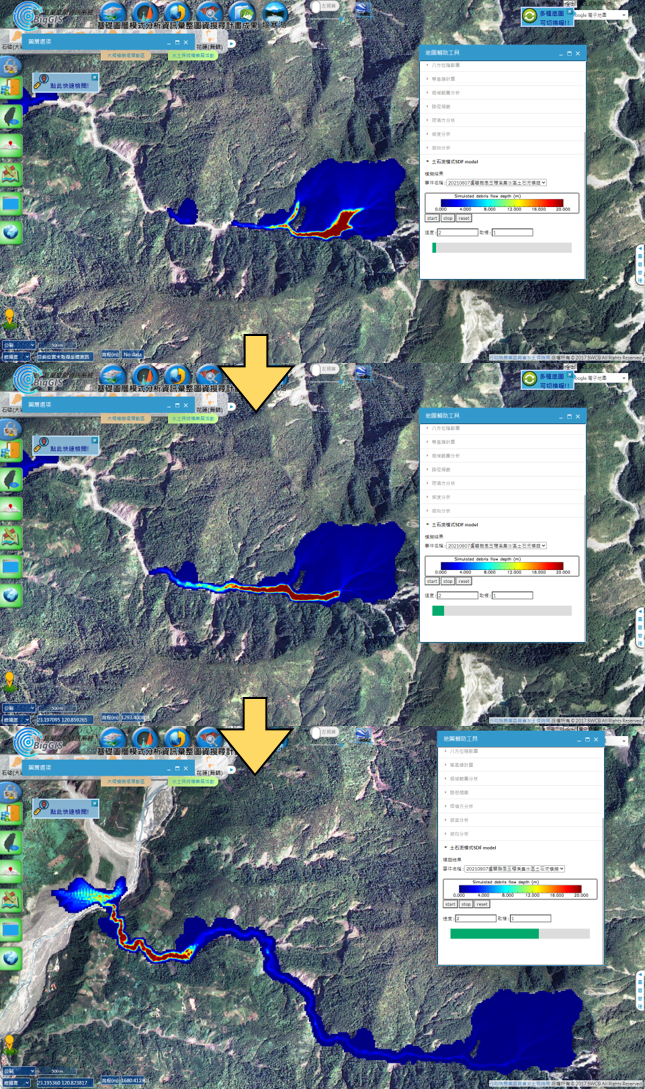
圖4 在BigGIS上瀏覽盧碧颱風玉穗溪集水區土石流模擬結果
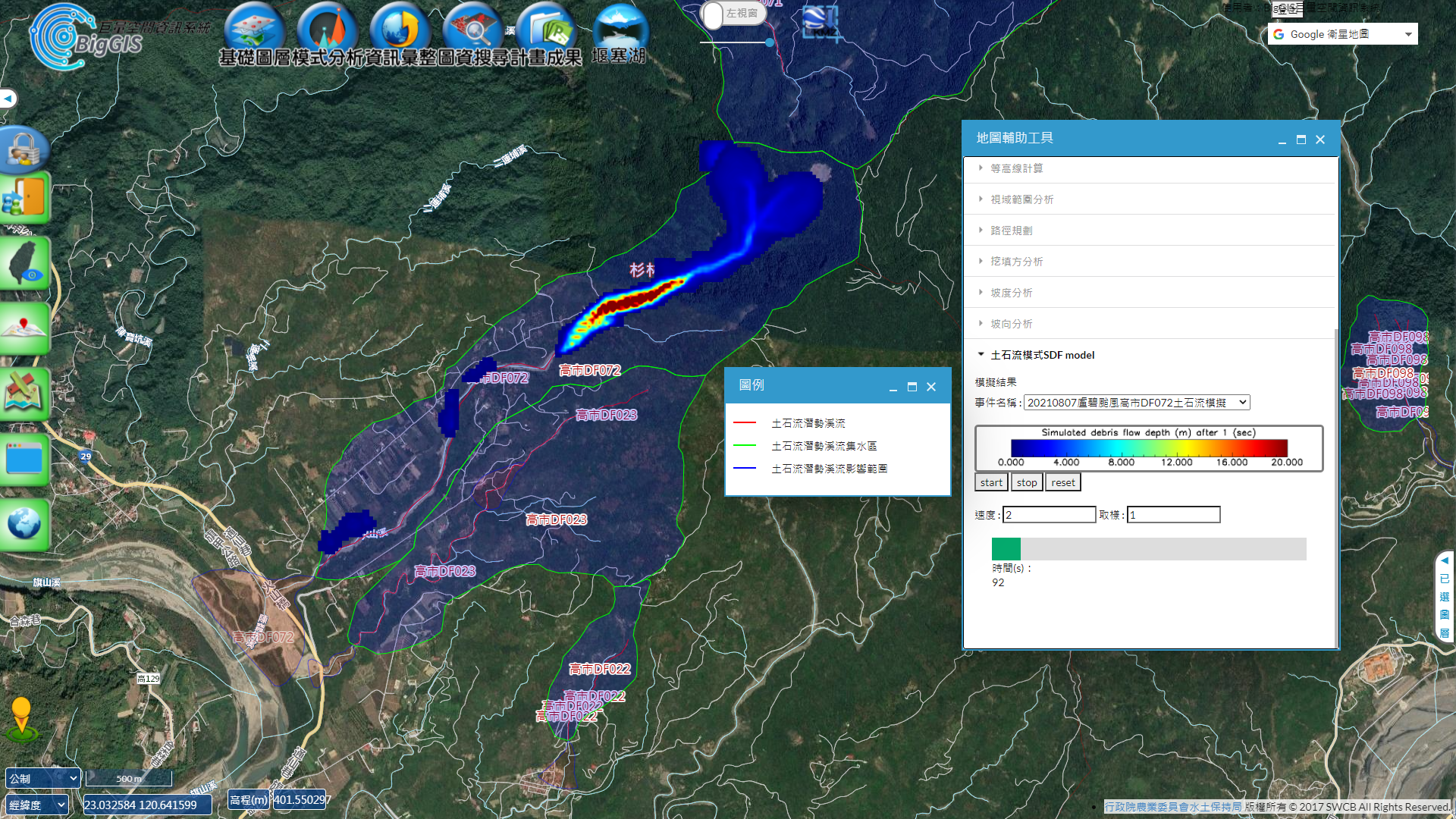
圖5 盧碧颱風旗山溪流域-火山溪土石流模擬結果在BigGIS上套疊其他圖資包含土石流潛勢溪流,影響範圍和集水區等
參考文獻
1.Chen, Y.-C., Wu, Y.-H., Shen, C.-W., & Chiu, Y.-J. (2018). Dynamic modeling of sediment budget in Shihmen Reservoir Watershed in Taiwan. Water, 10, 1808
2. Chiang, S.-H. (2010). 多重災害模擬-崩塌誘發及土石流. 臺灣大學地理環境資源學研究所學位論文, 1-134
3. Hunt, B. (1994). Newtonian fluid mechanics treatment of debris flows and avalanches. Journal of Hydraulic Engineering, 120, 1350-1363
4. Takahashi, T. (1981). Debris flow. Annual review of fluid mechanics, 13, 57-77


